23. Длина окружности и площадь круга. Шар
Номер 1.
Выполните практическую работу «Отношение длины окружности к диаметру» (см. рис. 3.44 учебника) и сделайте вывод по результатам заполнения последнего столбца.
| Радиус окружности R, мм |
Диаметр окружности d, мм |
Длина полоски – длина окружности С, мм |
Значение С : d (округлённое до сотых) |
| 20 | 40 | 124 | 3,10 |
| 25 | 50 | 156 | 3,12 |
| 30 | 60 | 188 | 3,13 |
| 35 | 70 | 221 | 3,16 |
| 40 | 80 | 252 | 3,15 |
| 45 | 90 | 280 | 3,11 |
1) С : d = 124 : 40 = 3,10
2) С : d = 156 : 50 = 3,12
3) С : d = 188 : 60 ≈ 3,133 ≈ 3,13
4) С : d = 221 : 70 ≈ 3,15714 ≈ 3,16
5) С : d = 252 : 80 = 3,15
6) С : d = 280 : 90 ≈ 3,1111 ≈ 3,11
Вывод: отношение длины окружности к диаметру всегда получается примерно 3,1.
Номер 2.
Полагая π ≈ 3,14, найдите длину окружности С, если известен её радиус R:
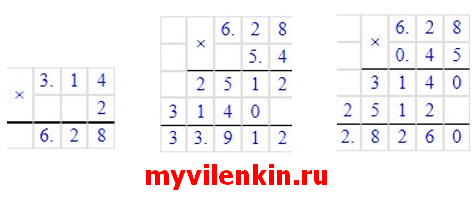
а) R = 10 см; С = 2πR ≈ 2 · 3,14 · 10 ≈ 62,8 (см)
б) R = 5,4 дм; С = 2πR ≈ 2 · 3,14 · 5,4 ≈ 33,912 (дм)
в) R = 0,45 м; С = 2πR ≈ 2 · 3,14 · 0,45 ≈ 2,826 (м)
Номер 3.
Полагая π ≈ 3,14, найдите длину окружности С, если известен её диаметр d:
а) d = 8,7 дм; С = πd ≈ 3,14 · 8,7 = 27,318 (дм)
б) d = 0,36 дм; С = πd ≈ 3,14 · 0,36 = 1,1304 (дм)

Номер 4.
Принимая π ≈ 3, найдите площадь круга S с радиусом R:
а) R = 1,2 дм; S = πR2 ≈ 3 · (1,2)2 = 3 · 1,44 = 4,32 (дм2)
б) R = 0,08 м; S = πR2 ≈ 3 · (0,08)2 = 3 · 0,0064 = 0,0192 (м2)
Номер 5.
Принимая π ≈ 3, найдите площадь круга S если его диаметр d равен:
а) 0,6 см; R = d : 2 = 0,6 : 2 = 0,3 (см), S = πR2 ≈ 3 · (0,3)2 =
= 3 · 0,09 = 0,27 (см2)
б) 14 м; R = d : 2 = 14 : 2 = 7 (м),
S = πR2 ≈ 3 · 72 = 3 · 49 = 147 (м2)